PERSAMAAN GARIS SINGGUNG LINGKARAN

PERSAMAAN GARIS SINGGUNG LINGKARAN 

A. PERSAMAAN LINGKARAN
Definisi

• Lingkaran adalah tempat kedudukan titik-titik yang berjarak sama terhadap dua titik tertentu.
• Titik tertentu disebut pusat lingkaran.
• Bagian yang berjarak sama disebut jari-jari. 

Bedasarkan kedudukan titik pusatnya, lingkran terdiri dua jenis, yaitu sebagai berikut.

 1. Lingkaran yang berpusat di O (0,0)

 

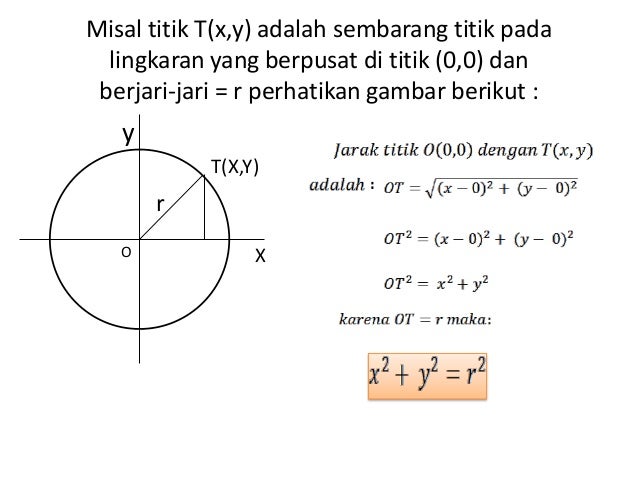
Contoh : Tentukan  persamaan lingkaran yang berpusat di (0,0) dan jari-jarinya 3?

Jawab : x² +  y² = r² 
                x² + y² = 3^{2
                 x2 + y2 = 9}

 

2. Lingkaran yang berpusat di (a,b)

 

Persamaannya :  r²=(x- a)² + (y – b)²

                                           ^atau

                                    ^{(x- a)2 + (y – b)2 = r2} 

^{Contoh :  Diketahui lingkarang berpusat di (2,3) dan berjari-jari 5. Persamaan lingkaannya adalah?}

^{Jawab : Dik : a = 2, b = 3, r = 5}

             ^{(x- a)2 + (y – b)2 = r2} 

             (x- 2)² + (y – 3)² = ⁵²

             ^{(x - 2)(x - 2) + (y – 3)(y - 3) = 25}  

             ^{x2 - 2x -2x + 4+ y 2 - 3y - 3y + 9 = 25}

             ^{x2 - 4x + 4+ y 2 - 6y + 9 = 25}

          ^{x2 + y 2 - 4x + 6y + 4 + 9 = 25}

            ^{x2 + y 2 - 4x + 6y +  13= 25}

            ^{x2 + y 2 - 4x + 6y +  13 -- 25= 0}

                ^{x2 + y 2 - 4x + 6y - 12= 0}

 ^{B. PERSAMAAN UMUM LINGKARAN}

 Lingkaran yang berpusat di P (a,b) dan berjari-jari

          

 (x- a)² + (y – b)² = r²
 x² – 2ax + a² + y² – 2by + b² = r² 

 x²+ y² – 2ax – 2by + a²+ b²– r² = 0 

 x²+ y² + Ax + By + C= 0

^{Dengan :}

^{Titik pusat ⇨}  

 Jari-jari lingkaran        

C. KEDUDUKAN GARIS TERHADAP LINGKARAN.

Penjelasan : (i)   Garis tidak menyinggung syarat D<0
                       (ii)  Garis menyinggung lingkaran syarat D=0
                       (iii) Garis memotong lingkaran syarat D>0
Contoh : Tentukan kedudukan garis y=x+1  terhadap lingkaran x²+ y² – 2x - 4y - 13= 0 !
              
Jawab :Dik : G ≡ y= x + 1 
                         L ≡ x²+ y² – 2x - 4y - 13= 0
 y= x + 1 disubtitusikan ke L  
x²+( X + 1⁾² – 2x + 4( X + 1⁾² - 13= 0
x²+ X² +2x + 1 - 2X  - 4X - 4 - 13= 0
2x² - 4x  - 16= 0 dibagi 2
x² – 2x - 8  = 0 ⇒ a= 1, b= -2, c= -8

a) D = b² - 4. a.c
        = (-2)² - 4. 1. (-8)
        = 4 + 32
        = 36 (garis menyingung D>0)

b) x² – 2x - 8  = 0
  (x + 2)(x - 4) = 0
  x = -2 atau x = 4
 Untuk x = -2⇒  y = x + 1 = -2 +1 = -1

 Untuk x = 4 ⇒ y= 4 + 1 =  5
Jadi, garis dan lingkarang potongan di titik (-2,1) dan (4,5)

D. PERSAMAAN GARIS SINGGUNG PADA LINGKARAN

• Persamaan garis singgung lingkaran x² +  y² = r²  yang melalui titik P (x1,y1) dapat di rumuskan :

x1.x + y1.y = r²

• Persamaan garis singgung lingkaran ^{(x- a)2 + (y – b)2 = r2} melalui titik P (x1,y1) dapat dirumus :

(x1 - a) (x - a) + (y1 - b) (y -b) = 0

• Persamaan garis singgung lingkaran  x²+ y² + Ax + By + C= 0 melalui titik P (x1,y1) dapat di rumuskan :

x₁x + y₁y + A(x₁ + x) + B(y₁ + y) + C = 0

                                                                     2                   2

Contoh : 

• Tentukan persamaan garis singgung dari lingkaran L ≡ (x - 3)²+ (y - 1)²  = 25 melalui titik (7,2) 

Jawab :Dik :  x1 = 7, y1 =2 
            (x1 - 3) (x - 3) + (y1 - 1) (y -1) =25
            (7- 3) (x - 3) + (2 - 1) (y -1) =25
            4x - 12 + y - 1 = 25
           4x + y - 12 - 1 =25
           4x + y - 13 = 25
           4x - y - 38 = 0 

• Diketahui x² +  y² = 10 melalui titik (-3,1) tntukan persamaan garis singgung ? 

Jawab : Dik : x1 = -3, y1 = 1 

             x1.x + y1.y = r² 

            -3.x + 1.y = 10

            -3x + 1y =10 

• Carilah persamaan garis singgung lingkaran x² +  y² + 4x - 6y + 3 = 0 melalyi titik (1,2)

Jawab : Dik : x1 = 1
                       y1 = 2
                      x² +  y² + 4x - 6y + 3 = 0 
    x₁x + y₁y + A(x₁ + x) + B(y₁ + y) + C = 0

                         2                  2

    1x + 2y + 4(x₁ + x) + -6(2 + y) + 3 = 0

                      2                  2

    1x + 2y + 2 + 2x + (-6) + (-3y) + 3 = 0
    3x - y + 5-6 =0
    3x - y - 1 = 0
E. Persamaan garis singgung pada lingkaran dengan gradien tertentu.

•  Persamaan lingkaran dengan pusat (0,0) adalah x2 + y2 = r2

Garis singgung pada lingkaran ini adalah

• Persamaan lingkaran dengan pusat (0,0) adalah (x – a)2 + (y – b)2 = r2

Garis singgung pada lingkaran ini adalah

tentukan

Contoh : 

Tentukan persamaan garis singgung lingkaran x² + y² = 25 yang tegak lurus garis 2y − x + 3 = 0 adalah....

Pembahasan
Garis 2y − x + 3 = 0 memiliki gradien sebesar ¹/₂. Garis lain yang tegak lurus dengan garis ini harus memiliki gradien − 2.

• m₁ ⋅ m₂ = − 1
  
  Sehingga persamaan garis singgung di lingkaran x² + y² = 25 yang memiliki gradien −2 adalah:
  
   

•  Persamaan garis singgung pada lingkaran x² + y² − 2x + 4y − 220 = 0 yang sejajar dengan

 garis 5 y + 12x + 8 = 0 adalah...

Jawab

Lingkaran x² + y² − 2x + 4y − 220 = 0 memiliki pusat:


dan jari-jari


Gradien garis singgungnya sejajar dengan 5 y + 12x + 8 = 0, jadi gradiennya adalah −12/5.

Persamaannya:

Sehingga dua buah garis singgungnya masing-masing adalah
 

 F. Manfaat persamaan garis singgung lingkaran

      Persamaan lingkaran seringkali digunakan untuk menyelesaikan permasalahan sehari-hari. Pada bagian ini akan dibahas mengenai penerapan persamaan lingkaran dalam jangkauan siaran radio dan gempa bumi, serta radar lainnya.